Wenger can aspire to a glorious Spring run-in
By Brian Sears
15 January 2010
If the second half of this season is as good for Arsenal as the second half of last season, they’ll win the title. That’s the hope that Arsene Wenger will be nurturing into the Spring, and we can paint a statistical scenario where it might just happen. Here’s how . . .
First of all, consider what happened to each team in the first half of last season. How many points did they win? How many did they win in the second half of the season? What was the increase (or decrease) in performance level? And when applied to this season, what happens next?
Some teams tend to follow patterns: Manchester United are typically steady then improve to a strong finish. Aston Villa fans will know to look away now, because they rush from the blocks, then stagger through the second half of the season.
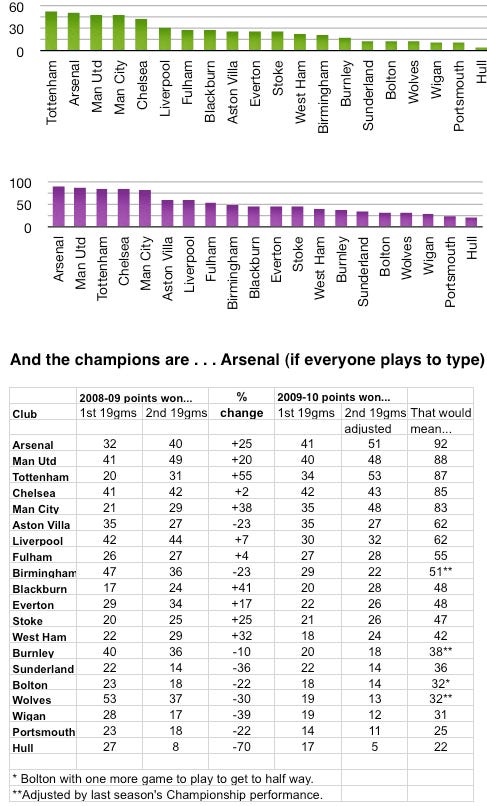
Looking at specific examples, Arsenal won 32 points in the first half of last season, then 40 in the second half, a performance increase of 25 per cent. United increased by 20 per cent from 41 points to 49, while Villa slumped 23 per cent with 35 points then 27. Hull faded most dramatically, amassing 27 points, and then a pitiful eight, a drop-off of 70 per cent.
To arrive at the conclusion that Arsenal can take the crown, we’ve applied last season’s second-half-of-the-season increase or decrease in performance to this season’s points tallies at half way.
In the top (green) graph below, you’ll see who would amass what extra points if everyone "played to type". Tottenham did 55 per cent better in the second half of last season, so with a 55 per cent increase again this time, they'll win 53 points from the last 19 games, and 87 altogether. Arsenal will add 51, United will add 48, and so on.
The next (purple) table is the season-end total if this particular footballing fantasy comes to fruition, making Arsenal champions ahead of United, Tottenham and Chelsea, with Man City and Villa next, and Liverpool seventh. Wigan, Portsmouth and Hull will go down by this reckoning. Our full set of permutations are in the table at the bottom.
.